Como Calcular Sacar Ángulos de Triángulo Conociendo Sabiendo sus Lados Teorema Coseno Ley Seno [18]

En este video, exploraremos cómo calcular los ángulos de un triángulo cuando se conocen las medidas de sus tres lados. Aprenderemos a aplicar la Ley de Cosenos para encontrar los ángulos internos con precisión. Además, descubriremos cómo el Teorema de Senos puede proporcionarnos otra perspectiva para determinar estos ángulos. Este conocimiento es fundamental para la trigonometría y la resolución de problemas prácticos.

¡Un viaje educativo hacia la comprensión de la geometría de los triángulos!

Cómo se pueden determinar los ángulos de un triángulo si se conocen las longitudes de sus lados
Cuáles son las fórmulas o métodos utilizados para encontrar los ángulos de un triángulo cuando se conocen los lados
Como se aplica el teorema del coseno para encontrar los ángulos de un triángulo
Cual es la fórmula de la ley del coseno y de la ley del seno para encontrar los ángulos de un triángulo cuando se conoce la longitud de uno de sus lados
Cuál es la ley de los senos y en qué situaciones se aplica
Cuál es el teorema del coseno y cómo se utiliza en problemas de trigonometría
Cómo se resuelve un triángulo usando la ley de los senos
Cómo se resuelve un triángulo usando el teorema del coseno

¡Bienvenidos a nuestro canal de matemáticas Mosta Profe! En este video, aprenderemos cómo calcular los ángulos internos de un triángulo de dos maneras diferentes. En primer lugar, utilizando el teorema del coseno, y en segundo lugar aplicaremos el teorema del coseno y la ley de los senos.

En primer lugar, repasaremos brevemente el teorema del coseno. Este teorema establece que, en un triángulo, el cuadrado de un lado es igual a la suma de los cuadrados de los otros dos lados menos el doble del producto de esos lados por el coseno del ángulo opuesto.
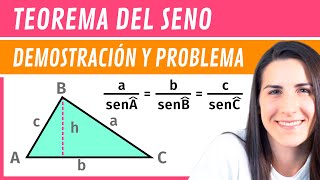
A continuación, tomaremos un triángulo ABC, cuyos lados son AB, BC y AC. Utilizando el teorema del coseno, podremos calcular los ángulos internos A, B y C.

En segundo lugar, repasaremos rápidamente el teorema de los senos. Este teorema establece que en cualquier triángulo, la proporción entre un lado y el seno del ángulo opuesto a ese lado es constante. Es decir:
a/sen(A) = b/sen(B) = c/sen(C)
Donde "a", "b" y "c" son las longitudes de los lados del triángulo, y "A", "B" y "C" son los ángulos opuestos a esos lados, respectivamente.

Paso 1: Identificaremos los lados y los ángulos conocidos del triángulo.
Paso 2: Usaremos el teorema de los senos para establecer una ecuación que relacione los lados y los senos de los ángulos.
Paso 3: Resolveremos la ecuación para encontrar el valor del ángulo desconocido.

Explicaremos paso a paso cómo aplicar las fórmulas.

¡Prepárate para mejorar tus habilidades matemáticas y tu conocimiento sobre el cálculo de ángulos en triángulos!

#MostaProfe #ResolverTriangulos #ResolucionDeTriangulos #AngulosInternos #LeyDeCosenos #LeyDeSenos #Triangulos #Angulos #Matemáticas #GeometríaAnalítica

★★★★★ Suscríbete, Manita Arriba 👍y toca la campana 🔔 para recibir notificación cuando subamos contenido nuevo.