Class 14. Bi Directional Associative Memory (BAM)

In the 14th lecture of his Soft Computing series, Dr. Aswani Kumar Cherukuri covers Bi-Directional Associative Memory (BAM) and expands on pattern association concepts.


This lecture, titled "Class 14: Bi-Directional Associative Memory (BAM)," is an in-depth session on advanced pattern association techniques within neural networks. It builds upon previous concepts of auto-associative and hetero-associative memory.
Key Topics Covered
1. Review of Associative Memory
Auto-association: Associating a pattern with itself. The lecture reiterates that for a network to store multiple patterns (the "capacity"), the patterns must be mutually orthogonal (their dot product must be zero) [04:19].
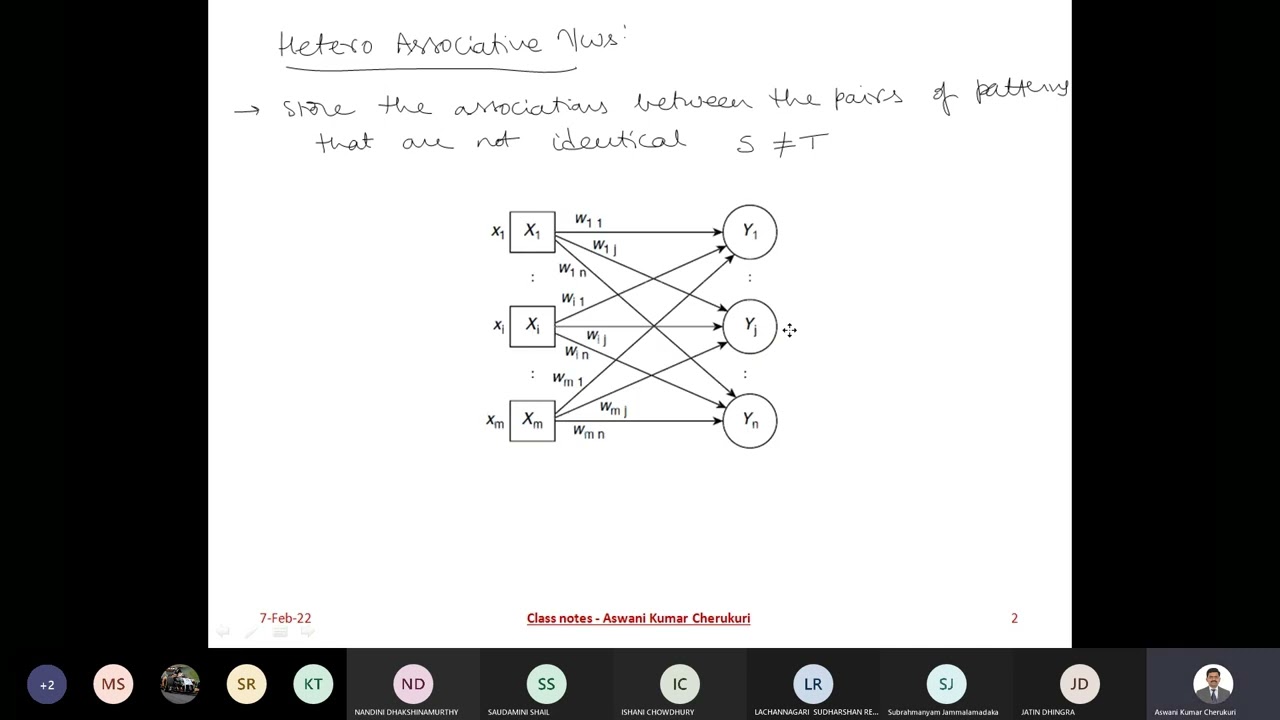
Hetero-association: Storing associations between different pairs of patterns (s \neq t). The architecture involves two layers (X and Y), and the weight matrix is calculated using the outer product of the pattern pairs [08:35].
2. Bi-Directional Associative Memory (BAM)
Definition: BAM is a hetero-associative model that allows information to flow in both directions. You can provide an input stimulus to get a response, or provide that response as a stimulus to retrieve the original input [16:52].
Architecture: Consists of two interconnected layers where activations can move forward (X \to Y) and backward (Y \to X) [19:42].
Weight Matrices:
For the forward direction (X \to Y), the weight matrix W is used.
For the backward direction (Y \to X), the transpose of the weight matrix (W^T) is used [21:26].
Bipolar Patterns: The instructor notes that bipolar patterns (using -1 and 1) are generally preferred over binary patterns (0 and 1) because they offer better generalization [23:16].
3. Practical Applications and Examples
Case Study (E and F Patterns): The lecture walks through a complex example of storing the letters 'E' and 'F'.
Patterns are represented by stars (1) and dots (-1) [31:56].
The instructor explains how to calculate individual weight matrices for each letter and sum them to create the final memory [34:59].
Testing involves presenting 'E' to get its target, then presenting the target to W^T to see if the network correctly recalls 'E' [35:50].
4. Algorithm Summary
The session concludes with a procedural overview:
Initialize weight matrices (often using the Hebbian rule or outer product).
For forward recall: Multiply input by W and apply an activation function.
For backward recall: Multiply the response by W^T to retrieve the original stimulus [37:34].