This Simple Trig Integral Is Trickier Than It Looks
Автор: Calculus Diaries
Загружено: 2025-12-30
Просмотров: 503
In this video, we evaluate the integral of tan(x)*sqrt(sec(x)+tan(x)) dx using a clever substitution that turns a messy trigonometric expression into a surprisingly clean result. This problem looks simple at first glance, but it hides a beautiful trick that makes the integration almost effortless once you see it.
The hurdle lies in expressing tan(x) and sec(x) in terms of the new substitution variable. I rely on the identity that sec^2(x)-tan^2(x) = 1, which is utilized along with the substitution, u^2=sec(x)+tan(x).
This type of integral frequently appears in advanced calculus, trigonometric substitution problems, and math competition settings. If you enjoy elegant calculus techniques and smart substitutions, this video is for you.
Subscribe to Calculus Diaries for beautifully explained calculus problems, clever integration tricks, and competition-style questions.
#calculus #integralcalculus #integrationtechniques #integration #trigonometricalidentities #maths
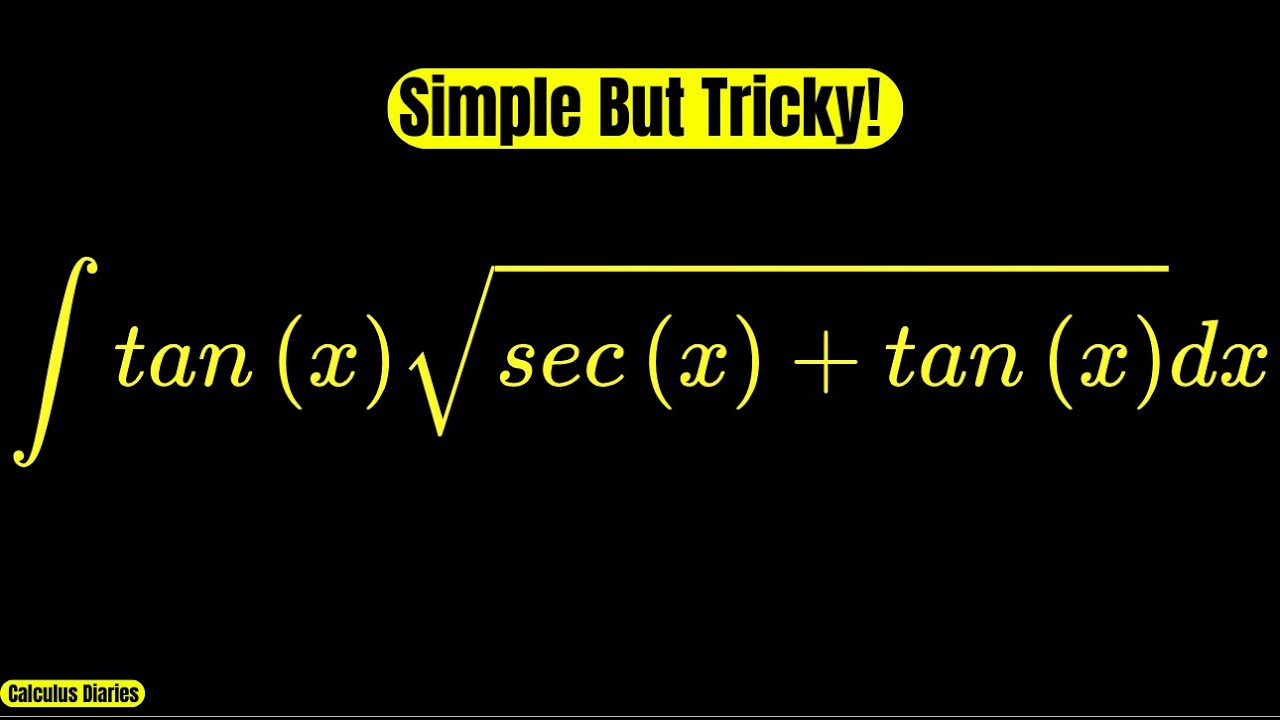
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:



















