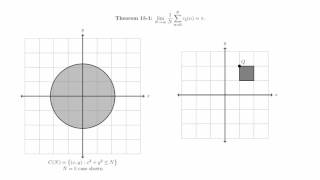
Mathematics - Lattice points on a circle on coordinate plane
Автор: John Morse
Загружено: 2013-09-21
Просмотров: 5697
Lattice points on a circle: First, find a suitably small whole number that can be expressed as the sum of two squares in 3 or more ways (so as to maximize number of lattice points). E.g., 325 does nicely, as it equals 18^2 + 1^2 and 15^2 + 10^2 and finally 17^2 + 6^2. Then, construct the circle from x^2 + y^2 = 325 and plot the lattice points, noting the symmetries among them - changes of signs, etc. For more variety of the points' coordinates, move the circle's center off the origin.

Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке: