The mysterious of Imaginary number "i"

Did you know the imaginary number i was born out of pure curiosity? From Cardano’s bold ideas to Bombelli’s daring math—this symbol changed everything we thought we knew about numbers.

Imaginary Numbers: The Numbers That Changed Reality

Imaginary numbers might sound fictional, but they are very real—and essential to modern science and technology.

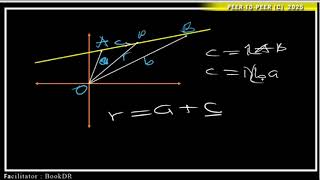
An imaginary number is defined as a number that gives a negative result when squared. The most basic imaginary unit is i, where:

i² = -1

For centuries, mathematicians thought it was impossible to take the square root of a negative number. But in the 16th century, Italian mathematicians like Gerolamo Cardano introduced the concept to solve polynomial equations, even though they called them “sophistic” or “useless” at first.

These numbers got their name from René Descartes in 1637, who used the term imaginary to criticize them. Ironically, today they're used in everything from quantum physics, electrical engineering, signal processing, to fractal geometry and computer graphics.

In mathematics, imaginary numbers are combined with real numbers to form complex numbers (a + bi). These complex numbers allow us to solve equations that have no real solutions—like x² + 1 = 0.

One fascinating fact: in electrical engineering, we use j instead of i, because i is already used for electric current. So, imaginary voltage or impedance values are labeled with j.

Even more surprisingly, some of the most beautiful equations in mathematics involve imaginary numbers—like Euler’s identity:

e^(iπ) + 1 = 0

This single equation connects five of the most important constants in mathematics: e, i, π, 1, and 0.

In short, imaginary numbers expanded our number system beyond the real line, helping us describe rotation, waveforms, and dynamic systems in ways that real numbers alone never could.

They may be called “imaginary,” but without them, much of our real-world technology wouldn’t exist.

#ImaginaryNumbers #MathFacts #ComplexNumbers #EulerIdentity #STEMeducation #MathIsBeautiful #ScienceExplained #MathShorts #QuantumMath #EngineeringMath