A Tangential Pentagon with Unequal Sides | 2020 AIME Problem-13 | RitwikMath
Автор: RitwikMath
Загружено: 2026-01-16
Просмотров: 18
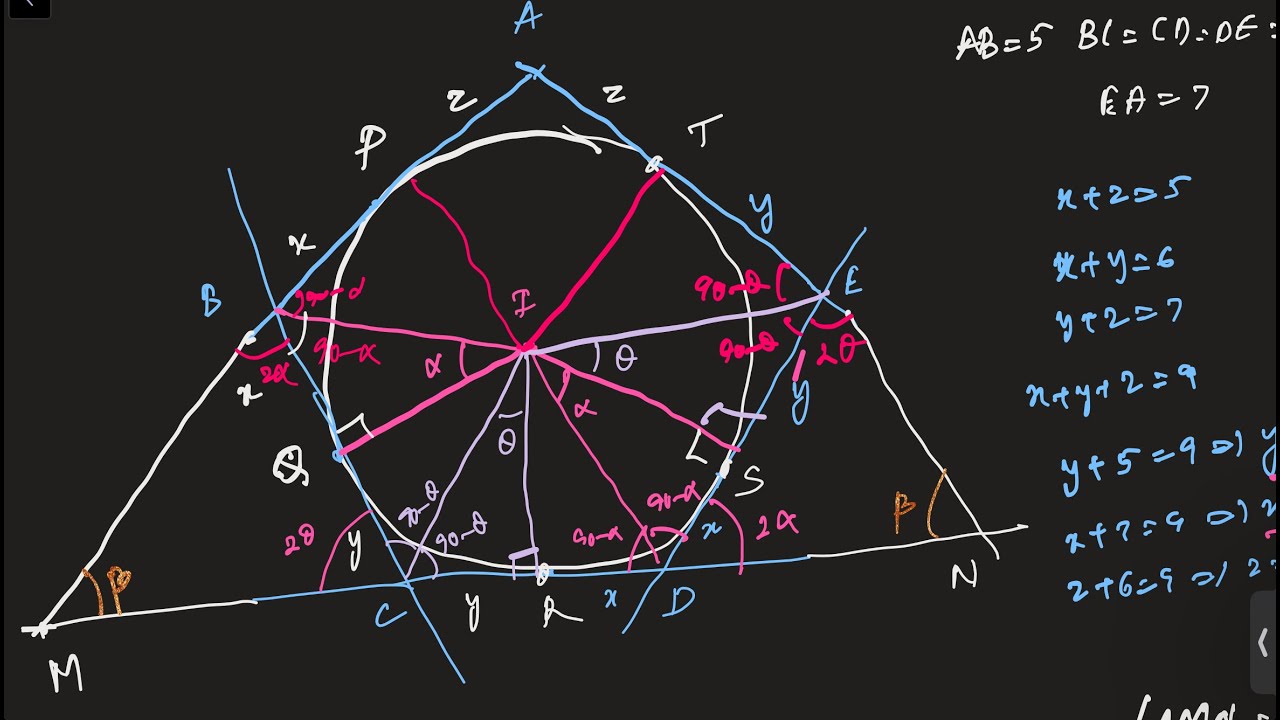
This elegant AIME-style geometry problem explores a convex pentagon with fixed side lengths and the special property of having an *incircle* (a circle tangent to all five sides). By applying equal tangent segment properties, triangle congruences (SAS and AAS), angle chasing, and the Law of Cosines, the solution constructs auxiliary points and triangles that reveal deep geometric symmetry.
The problem culminates in a clever **area decomposition**, where the area of the pentagon is found by subtracting the areas of congruent triangles from a larger constructed triangle—an approach frequently seen in advanced math olympiad problems.
🏁 Final Answer
\[
\boxed{60}
\]
Solution Reference (-Fanyuchen20020715): https://artofproblemsolving.com/wiki/...
#AMC #AIME #INMO #RMO #IOQM #BMO #CEMC
#MathOlympiad #OlympiadGeometry #EuclideanGeometry
#Incircle #TangentialPolygon #ContestMath
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:















