Доказательство формул суммы-разности. Часть 1
Автор: MasterWuMathematics
Загружено: 2015-07-02
Просмотров: 31646
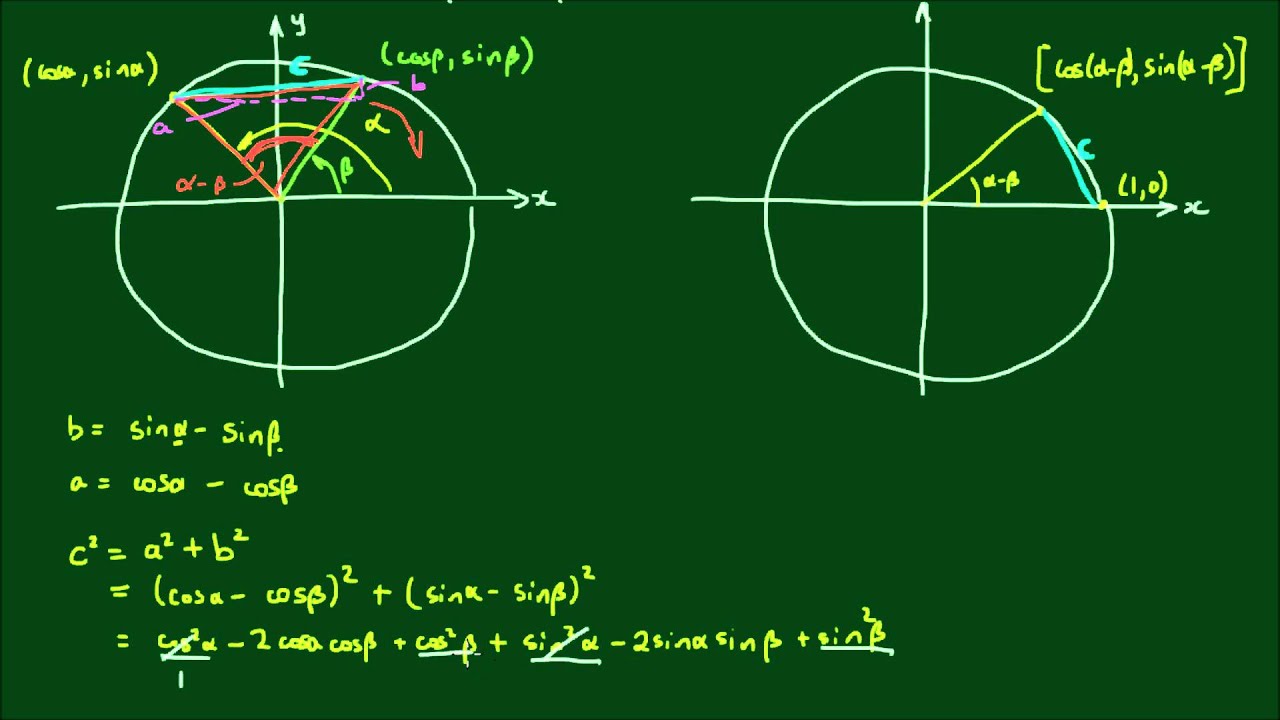
В этом видео я показываю, как доказать следующие формулы суммы-разности, или тригонометрические тождества:
cos(a - b) = cos(a)*cos(b) + sin(a)*sin(b)
cos(a + b) = cos(a)*cos(b) - sin(a)*sin(b)
sin(a + b) = sin(a)*cos(b) + sin(b)*cos(a)
sin(a - b) = sin(a)*cos(b) - sin(b)*cos(a)
Из приведённых выше результатов я также вывожу следующие тождества:
cos(2a) = cos^2(a) - sin^2(a)
sin(2a) = 2*sin(a)*cos(a)
Спасибо за просмотр. Пожалуйста, поставьте «лайк», если это видео было вам полезно.
Пожалуйста, задайте мне вопрос по математике в комментариях ниже, и я постараюсь помочь вам в будущих видео.
Следуйте за мной в Твиттере! twitter.com/MasterWuMath
cos(x - y) = cos(x)*cos(y) + sin(x)*sin(y)
cos(x + y) = cos(x)*cos(y) - sin(x)*sin(y)
грех(х + у) = грех(х)*cos(y) + грех(х)*cos(y)
грех(x - y) = грех(x)*cos(y) - грех(x)*cos(y)
соз(2х) = соз^2(х) - грех^2(х)
грех(2х) = 2*грех(х)*cos(х)
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:

![1.6 Тригонометрические пределы [03] Доказательство sinx/x](https://image.4k-video.ru/id-video/vz9_102nL8M)

















