Przekształcanie wykresu poprzez symetrię względem osi OX i OY
Автор: MARTAmatics PL
Загружено: 2020-03-25
Просмотров: 80559
#matematyka #matura #funkcje #przekształcenia #wykres #symetria
Link do playlisty Funkcje: • Funkcje
Wyjaśniam, jak na podstawie wykresu funkcji y = f(x) naszkicować wykresy funkcji: y = -f(x), y = f(-x). Wykresy takich funkcji powstają przez przekształcenie wykresu funkcji y = f(x) poprzez symetrię osiową względem osi OX lub OY. Pokazuję, jak takie odbicia symetryczne wykresu funkcji względem osi OX i OY zmieniają jej wzór.
Tłumaczę, jak rozwiązać zadania maturalne:
Dany jest wykres funkcji y = f(x). Naszkicuj wykres funkcji y = -f(x), y = f(-x).
Wykres funkcji g otrzymamy, przekształcając wykres funkcji f(x) = x² - 3x + 1 przez symetrię osiową względem osi OX. Podaj wzór funkcji g.
Wykres funkcji g otrzymamy, przekształcając wykres funkcji f(x) = -|x| + 1 przez symetrię osiową względem osi OX. Podaj wzór funkcji g.
Wykres funkcji g otrzymamy, przekształcając wykres funkcji f(x) = x + 2 przez symetrię osiową względem osi OY. Podaj wzór funkcji g.
Wykres funkcji g otrzymamy, przekształcając wykres funkcji f(x) = x² - 2x + 3 przez symetrię osiową względem osi OY. Podaj wzór funkcji g.
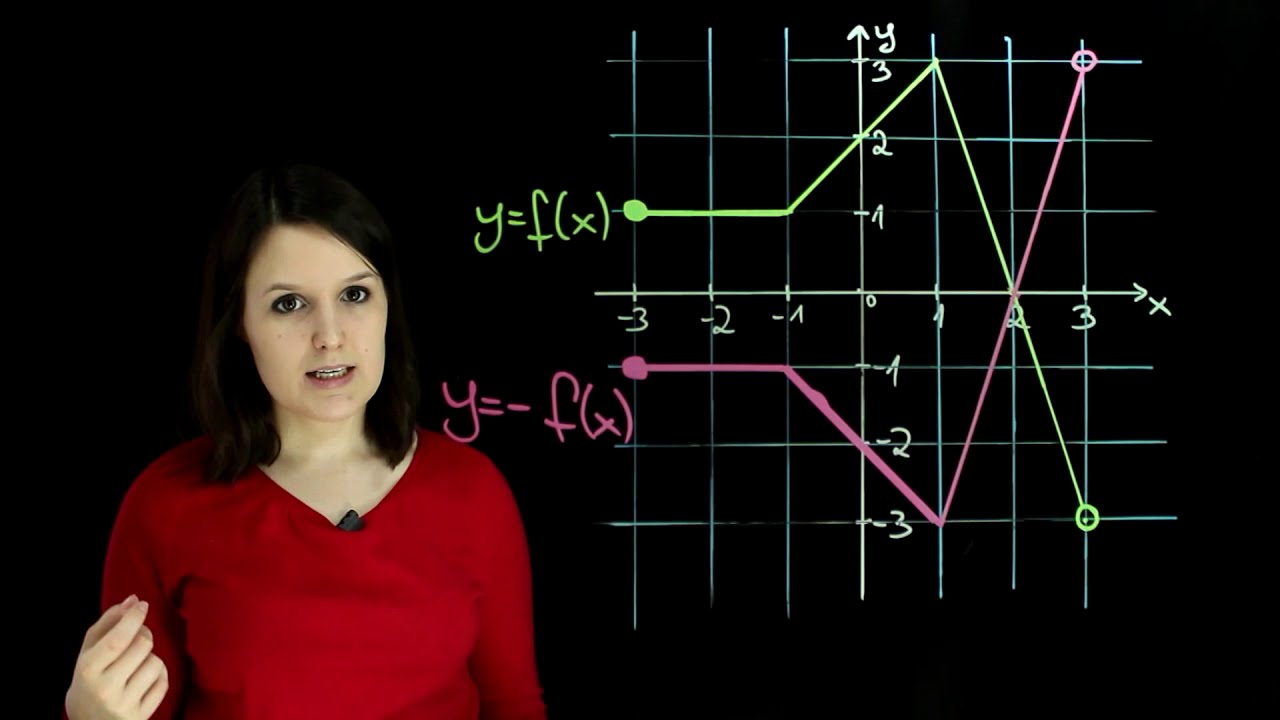
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:



















