How to Read a Venn Diagram: ‘At Least One’ & ‘Neither’ Explained Katie Rowlands

Summary of Video Content on Venn Diagram Problem Solving
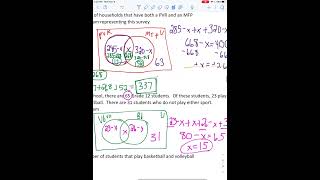
The video presents a detailed explanation on how to solve a classic problem involving Venn diagrams with two sets: people who like Maths and people who like Science. The total number of people surveyed is 30. The problem requires determining how many people like at least one of the subjects, how many like both, and how many like neither.

Core Concepts Explained
Venn Diagram Definition:
A Venn diagram consists of two or more circles representing different sets. Each circle includes elements belonging to that set, and overlapping sections represent elements common to multiple sets.

Sets in the Problem:

Maths set (left circle)
Science set (right circle)
Given Data:

18 people like Maths
15 people like Science
Total number of people surveyed: 30
10 people like both Maths and Science
Step-by-Step Solution Breakdown
Initial Setup:
Draw two intersecting circles, one representing Maths and the other Science.

Understanding the Overlap:
The sum of people liking Maths (18) and Science (15) is 33, which is greater than the total surveyed (30). This indicates an overlap — some people like both subjects.

Calculate the Overlap:
The problem states that 10 people like both Maths and Science. This overlap is the intersection of the two circles.

Calculate Exclusive Groups:

People who like only Maths (not Science) = 18 (total Maths) - 10 (both) = 8
People who like only Science (not Maths) = 15 (total Science) - 10 (both) = 5
Total People Who Like at Least One Subject:
Add the three groups:

Only Maths: 8
Both Maths and Science: 10
Only Science: 5
Sum = 8 + 10 + 5 = 23
People Who Like Neither Subject:

Total surveyed: 30
People liking at least one subject: 23
Therefore, people liking neither = 30 - 23 = 7
Quantitative Summary Table
Category Number of People Explanation
Like only Maths 8 18 total Maths - 10 both
Like only Science 5 15 total Science - 10 both
Like both Maths and Science 10 Given in the problem
Like at least one subject 23 8 + 10 + 5
Like neither Maths nor Science 7 30 total - 23 at least one
Key Insights and Conclusions
Overlap is essential in Venn problems: The sum of individual sets can exceed the total population because some individuals belong to both sets.

Starting with the intersection simplifies the problem: Knowing the number of people who like both subjects (the intersection) allows for the straightforward calculation of exclusive groups.

“At least one” means union of the sets: The total number of people who like either Maths or Science (or both) is the sum of only Maths, only Science, and both groups.

“Neither” is the complement of the union: People who like neither subject are those outside both sets.

Verification through addition: Adding the numbers in all sections (only Maths, only Science, both, and neither) should equal the total number of people surveyed.

Explanation of Terminology
Term Definition
Set A collection of distinct objects or elements (e.g., people who like Maths)
Intersection The set of elements common to both sets (people who like both Maths and Science)
Union The set of elements in either or both sets (people who like at least one subject)
Complement Elements not in a specified set (people who like neither Maths nor Science)
Additional Notes
The video emphasizes not to assume that the sum of individual sets equals the total population in such problems without considering overlap.

It also reinforces the importance of drawing the Venn diagram to visualize the problem clearly.

The explanation follows a logical progression from understanding the problem, setting up the diagram, calculating intersections and exclusive groups, to verifying totals.

The problem is an example of basic set theory applied to real-world survey data.

Summary
The video provides a comprehensive walkthrough of solving a Venn diagram problem involving two overlapping sets — Maths and Science preferences among 30 individuals. By identifying the number of people who like both subjects, the solution calculates exclusive group sizes, the total liking at least one subject, and those liking neither. The key takeaway is understanding overlaps and how they affect total counts, illustrated through clear numerical calculations and visual representation via a Venn diagram. This methodical approach ensures accurate problem-solving in set theory contexts.