Demystifying Hilbert Space
Автор: Gerard Meilan
Загружено: 2026-01-17
Просмотров: 10
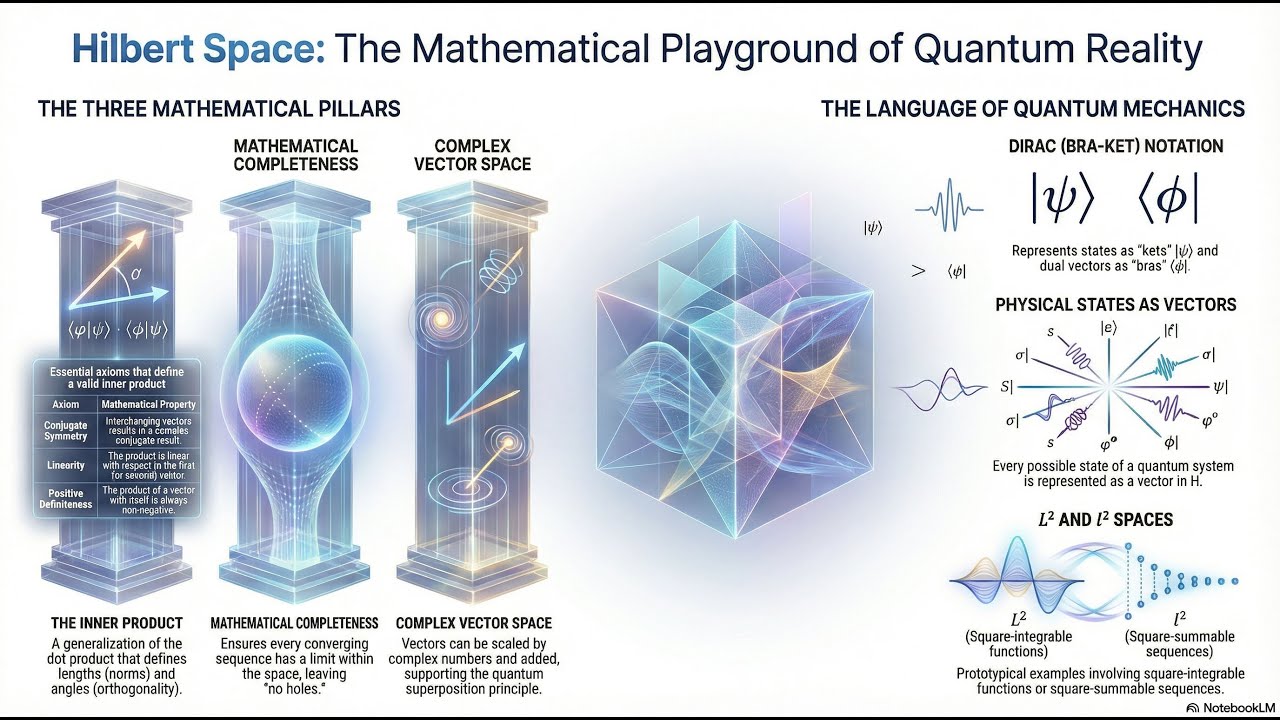
At its core, a Hilbert space is a complete linear vector space equipped with an inner product, serving as a generalization of Euclidean geometry to spaces with potentially infinite dimensions. The defining inner product structure allows for geometric concepts like length (norm), angle, and orthogonality to be rigorously applied to abstract objects such as functions or infinite sequences. Crucially, the "completeness" requirement ensures that the space contains all necessary limits—meaning every Cauchy sequence converges to an element within the space—which permits the use of calculus and analysis without the risk of "falling out" of the space. This unique combination of geometric structure and analytical completeness makes Hilbert space the essential mathematical framework for fields like signal processing and quantum mechanics, where physical states are represented as vectors within this space.
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:



![Суть линейной алгебры: #15. Быстрый способ найти собственные значения [3Blue1Brown]](https://image.4k-video.ru/id-video/njeRu8k8VhQ)















