DDPS | Dynamical approximation and sensor placement for the state estimation of transport problems

DDPS Talk date: April 11th, 2025

Speaker: Cecilia Pagliantini (University of Pisa, https://numpi.dm.unipi.it/people/ceci...)

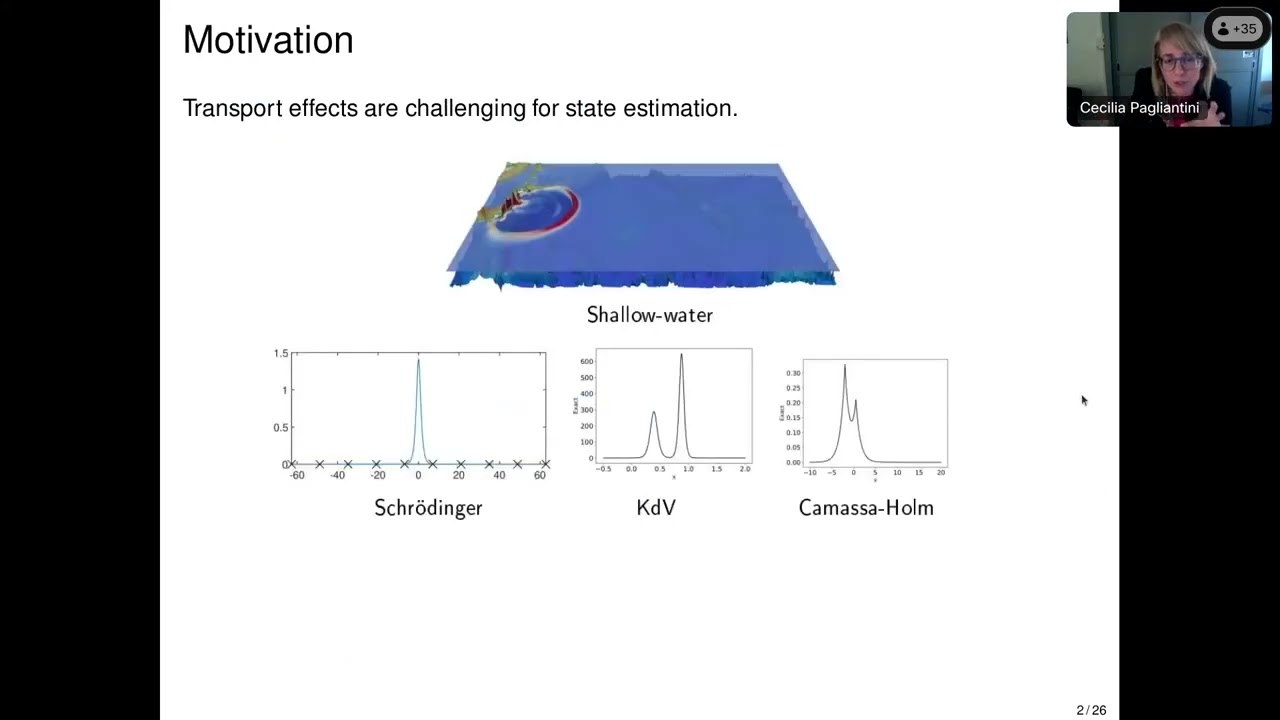
Description: This talk focuses on the inverse problem of reconstructing an unknown function $u$ from a finite set of measurements, under the assumption that $u$ is the output of a parametric differential equation with unknown input parameters. Typically, the target function $u$ belongs to an infinite-dimensional Hilbert space and the geometry of the solution set $M$ is not known a priori. One way to reduce the complexity of the problem is to approximate $M$ by a linear, finite dimensional subspace $V$ using model order reduction, and to search for an approximation $u^{\star}\in V$ to the state $u$. It is however known that such approach become ineffective for approximating the dynamics of transport problems. In this talk we will discuss how to address inverse problems for wave phenomena in the framework of Hamiltonian systems. The method combines symplectic dynamical low-rank approximation to update $V$ with dynamical placement of the sensors to ensure an accurate reconstruction at all times. This talk is based on joint work with Olga Mula (TU/e) and Federico Vismara (TU/e).

Bio: Cecilia Pagliantini is Assistant Professor in the Department of Mathematics at the University of Pisa, Italy. After obtaining her PhD at the Seminar for Applied Mathematics of ETH Zurich, Switzerland, she held postdoctoral positions at the Los Alamos National Laboratory, USA, and at the EPFL, Switzerland. She joined TU/e Eindhoven in 2020 as assistant professor in the Centre for Analysis, Scientific Computing and Applications (CASA) and moved to the University of Pisa in 2023. Her research focuses on the development, analysis and implementation of numerical methods for differential equations. In particular, she works on numerical discretizations and model order reduction able to yield approximate models possessing the same geometric structures and physical properties of the original models. She is also interested in robust numerical methods and efficient solvers for fluid and kinetic plasma physics, and for problems arising in computational electromagnetism.

DDPS webinar: https://www.librom.net/ddps.html
💻 LLNL News: https://www.llnl.gov/news
📲 Instagram:   / livermore_lab  
🤳 Facebook:   / livermore.lab  
🐤 Twitter:   / livermore_lab  

About LLNL: Lawrence Livermore National Laboratory has a mission of strengthening the United States’ security through development and application of world-class science and technology to: 1) enhance the nation’s defense, 2) reduce the global threat from terrorism and weapons of mass destruction, and 3) respond with vision, quality, integrity and technical excellence to scientific issues of national importance. Learn more about LLNL: https://www.llnl.gov/.

LLNL release number is: LLNL-VIDEO-2004816