Ford-Fulkerson and Edmonds-Karp: Finding the Maximum Flow

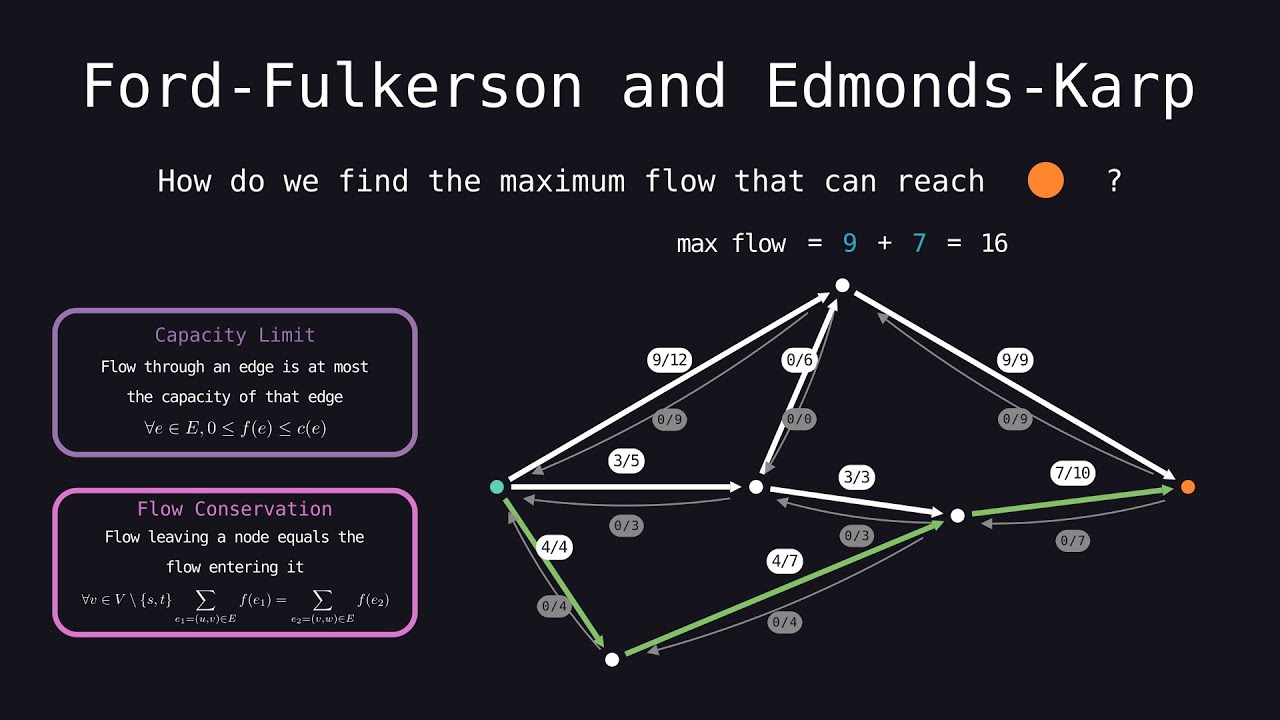
The total flow in a flow network is equal to the sum of the flow values on edges leaving the source, or the sum of the flow values on edges entering the sink. But what is the MAXIMUM flow that can reach the sink?

Code: https://github.com/emcapsulation/max-...

00:00 Introduction
00:36 Flow Networks
02:28 Counterexample
03:40 Ford-Fulkerson Walkthrough
06:08 Larger Example
08:14 Edmonds-Karp
09:06 Code
14:04 Code Demo

Algorithm Steps
1. While there are still paths from s to t, find an augmenting path from s to t. An augmenting path is a path you can push flow on, i.e. the bottleneck capacity is greater than 0.
2. Find the bottleneck capacity of this path, fb. This is given by the edge in the path which can have the least amount of flow pushed through it, restricting the flow of your entire path.
3. Push fb units of flow through the path. If the edge in the path is a forward edge, add fb units of flow to it. If the edge in the path is a backward edge, deduct fb units of flow from it.
4. Rebuild the residual graph. For each edge in the path, insert a back edge whose capacity is equal to the flow value of that edge.
5. When there are no more augmenting paths remaining, return the final flow as the maximum flow.

The Edmonds-Karp algorithm is an implementation of the Ford-Fulkerson method for finding the max flow. It uses a breadth-first search to find the augmenting paths from s to t. Its time complexity is O(m^2 n).