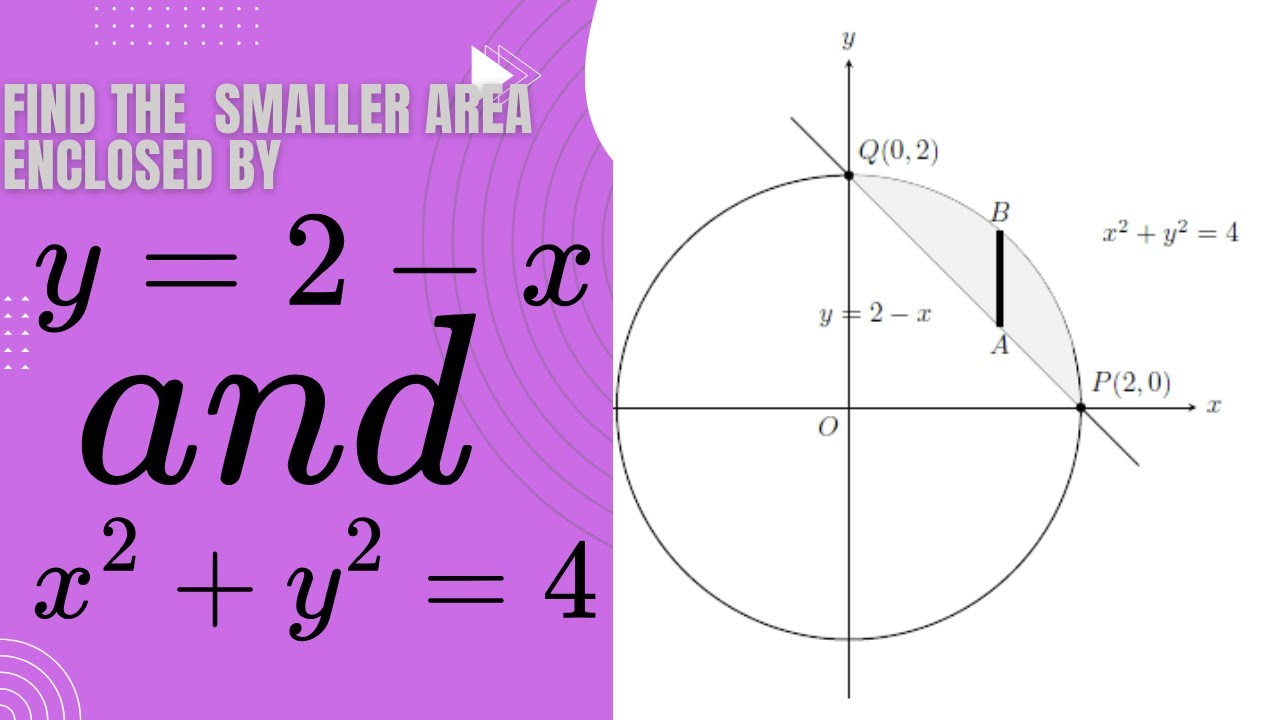
Areas in Cartesian plane prb5/ Beyond Rectangular: Finding the Enclosed Area of y=2-x & x²+y²=4

Areas in cartesian Co-ordinates Problem 5/JNTU Engineering maths
Unpacking the Intersections: Defining Our Boundaries
To precisely define our integration limits, we need to find exactly where the line and the circle shake hands. These intersection points are crucial.
We'll use algebraic substitution to solve for these points, which will give us the x and y coordinates where our two equations meet.
Understanding these points is key to choosing the correct order of integration – do we integrate with respect to x first, or y? Let's explore the implications.
Setting Up the Integral: A Strategic Approach
Now that we know our boundaries, it’s time to set up the double integral. This is where we decide how to slice our region.
We'll analyze the region to determine if a dx dy or dy dx setup is more efficient and simplifies our limits of integration. Hint: sometimes one way is significantly easier!
We'll carefully construct our inner and outer limits, ensuring they accurately trace the perimeter of our enclosed area. This is the heart of the problem!