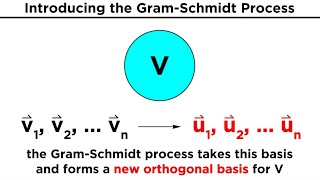
Процесс ортогонализации Грама-Шмидта: математическое объяснение.

Ортогонализация Грама-Шмидта — один из самых популярных методов линейной алгебры. Это алгоритм оптимизации для решения задачи наименьших квадратов в линейной регрессии. Идея процесса ортогонализации Грама-Шмидта заключается в поиске набора ортогональных матриц, который лучше соответствует предполагаемой модели, чем текущий набор матриц.
Процесс ортогонализации Грама-Шмидта может использоваться во многих областях, включая экономику, физику и инженерию. Если вам интересно узнать больше об этом процессе, продолжайте читать!

Процесс ортогонализации Грама-Шмидта: математическое объяснение.
Процесс ортогонализации Грама-Шмидта — один из самых популярных методов линейной алгебры. Это алгоритм оптимизации для решения задачи наименьших квадратов в линейной регрессии. Идея процесса ортогонализации Грама-Шмидта заключается в поиске набора ортогональных матриц, который будет лучше соответствовать предполагаемой модели, чем текущий набор матриц.

Процесс ортогонализации Грама-Шмидта может использоваться во многих областях, включая экономику, физику и инженерию. Если вам интересно узнать больше об этом процессе, продолжайте читать!

Что такое процесс ортогонализации Грама-Шмидта?
Процесс ортогонализации Грама-Шмидта — это процедура линейной алгебры. Этот процесс находит наилучший набор ортогональных матриц, который будет лучше соответствовать предполагаемой модели, чем текущий набор матриц.

Этот процесс появился в 1843 году, когда датский математик Расмус Бартолин разработал его как один из способов решения задачи наименьших квадратов в линейной регрессии. Проблема этого метода заключалась в том, что существовало множество способов вычисления решения методом наименьших квадратов, но ни один из них не был признан лучшим.

Процесс ортогонализации Грама-Шмидта был задуман как алгоритм, который выбирал бы наилучшее возможное решение этой задачи. Он помогает найти правильную матрицу, проверяя все возможные решения и выбирая те, которые имеют наибольшую остаточную дисперсию.

При использовании этого процесса необходимо иметь начальный набор ортогональных матриц, которые используются в качестве отправной точки. Затем можно вычислять новые ортогональные матрицы, используя алгоритм Грама-Шмидта, пока не будет достигнута сходимость, то есть когда изменение остаточной дисперсии становится ниже некоторого порогового значения после каждой итерации.

Как работает процесс ортогонализации Грама-Шмидта?
Процесс ортогонализации Грама-Шмидта — это алгоритм линейной алгебры, который может использоваться во многих различных областях. Этот процесс применяется, когда имеется два набора уравнений и один набор неизвестных. Цель — найти набор ортогональных матриц, который лучше соответствует предполагаемой модели, чем текущий набор матриц.

На первом этапе выбирается исходная матрица, которая служит основой для решения. Затем все столбцы этой матрицы умножаются на новую ортогональную матрицу, сгенерированную из предыдущего столбца, в котором каждый элемент заменен на комплексно-сопряженное число. Например, если бы у нас было:

A = (1 2 -1)

Мы могли бы переписать это как:

A' = (1 - 2i 1 + 2i)

Выполнив эти шаги, мы получим окончательный результат:

A'' = (1 - 4i 2 + 4i 0 0).

Применение процесса ортогонализации Грама-Шмидта
Как уже упоминалось, процесс ортогонализации Грама-Шмидта может использоваться во многих различных областях, включая экономику, физику и инженерию.

Одним из наиболее популярных примеров этого процесса является линейная регрессия. Процесс ортогонализации Грама-Шмидта часто используется в линейной регрессии для поиска набора ортогональных матриц, которые лучше соответствуют предполагаемой модели, чем текущий набор матриц.

Существует множество других применений этого процесса, не связанных с линейной алгеброй. Например, если требуется реализовать эффективный алгоритм поиска кратчайшего пути между двумя узлами графа с неравномерной стоимостью, можно использовать процесс ортогонализации Грама-Шмидта.

Заключение
Процесс ортогонализации Грама-Шмидта — это алгоритм для построения ортогональных матриц. Он широко используется в математике, инженерии и статистике.