DAA 03 – Matrix Multiplication Algorithms | Divide and Conquer & Strassen | CS F364

This lecture discusses matrix multiplication algorithms as part of the Design and Analysis of Algorithms (DAA) course (CS F364). We begin with the iterative (naïve) matrix multiplication algorithm, formally defining matrix multiplication and analyzing its Θ(n³) time complexity.

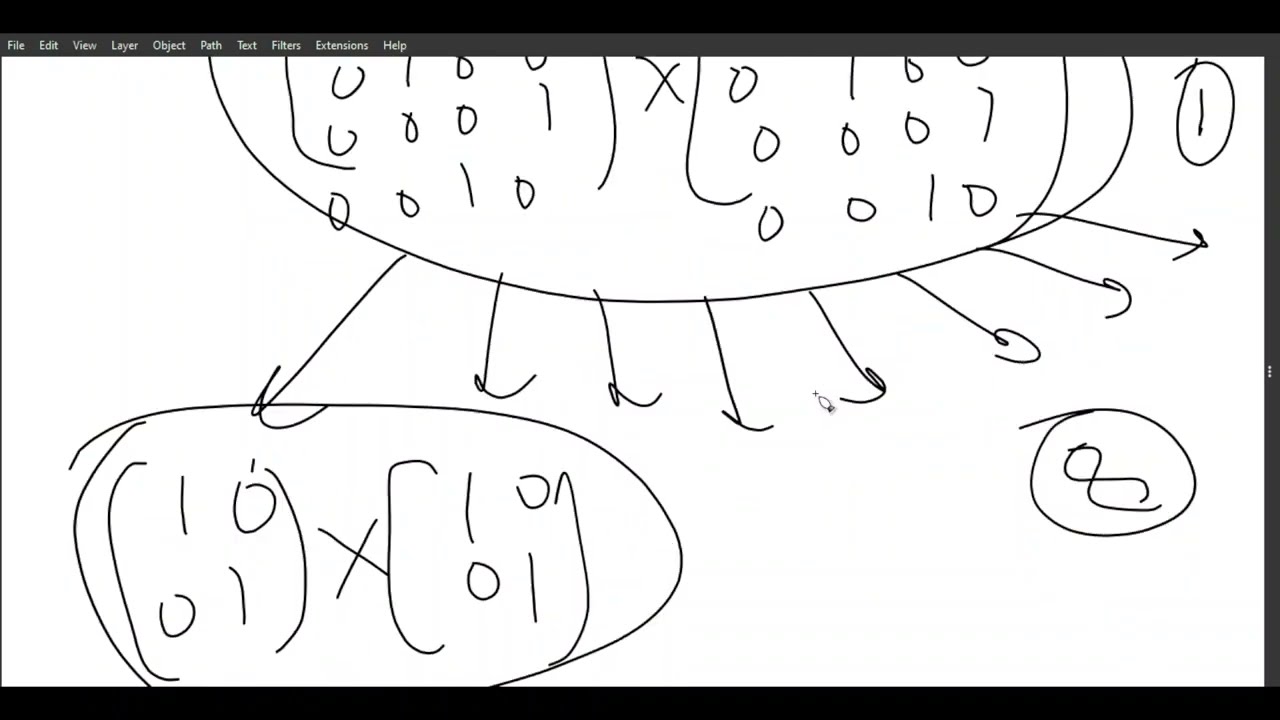
The lecture then introduces a divide and conquer approach to matrix multiplication, where matrices are recursively partitioned into submatrices. The recursive formulation is explained in detail, along with a recursion tree–based time complexity analysis.

Finally, we present Strassen’s matrix multiplication algorithm, an advanced divide and conquer technique that reduces the number of recursive subproblems from eight to seven. The lecture derives the recurrence relation for Strassen’s algorithm and solves it to obtain the improved Θ(n^{log₂7}) time complexity.

📌 Topics Covered in This Lecture

Definition of matrix multiplication

Iterative (naïve) matrix multiplication algorithm

Time complexity analysis of iterative matrix multiplication

Divide and conquer matrix multiplication

Recursive formulation and divide-and-conquer graph

Recursion tree analysis for matrix multiplication

Strassen’s matrix multiplication algorithm

Reduction from eight to seven subproblems

Recurrence relation for Strassen’s algorithm

Solving recurrences and final time complexity

🎯 Who Should Watch

Students studying Design and Analysis of Algorithms (DAA)

B.Tech / BE / MCA / M.Sc. (CS) students

Learners preparing for university examinations and GATE Computer Science

Anyone learning divide and conquer algorithms with recurrence analysis

🔗 Playlist

This video is part of the playlist:
Design and Analysis of Algorithms – Complete DAA Course