Laszlo Feher, part 1, "Polynomiality of Plücker numbers"

Title: Polynomiality of Plücker numbers

Abstract: Two of the classical Plucker problems are to determine the number of bitangents and flexes of a degree $d$ curve. For the generic case the answer (by Plücker in the 1830s) is 1/2 d(d-2)(d-3)(d+3) and 3d(d-2) respectively. If we want to study tritangents, etc, then we need to study degree d hypersurfaces in P^n. If the variety of tangent lines with the given multiplicity is higher dimensional, we can add a linear condition to obtain a number.

For example $2d(3d − 2)(d − 3)$ is the number of 4-flex lines to a generic degree $d$ surface in $P^3$ intersecting a given line.


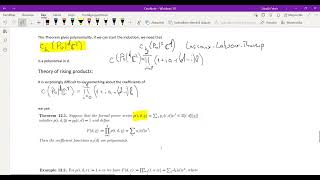
Though various algorithms were already available to calculate these numbers for a given $d$, they were not helpful to prove polynomiality and determining the degree of these polynomials. Using branched coverings of coincident root strata we determine the leading terms of these polynomials.

In the second part I talk about our original motivation, which was to calculate the Euler characteristics, and the $\Chi_y$-genera of these varieties of tangent lines. We developed ways to calculate them and proved that the Euler characteristics is also polynomial in $d$, and we conjecture that about the $\Chi_y$-genus as well.


The main tool is equivariant cohomology, CSM classes and motivic Chern classes. Along the work we realized that some of the classical problems have not been answered yet, so I mention some of the interesting ones.

Joint work with Andras P. Juhasz and Balazs Komuves.