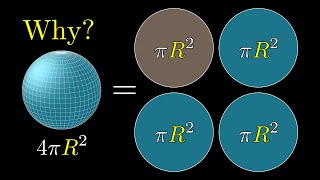Isoperimetric problems and its applications l Dido's problem l city of carthage l Mathspacetech

Isoperimetric problems and its applications l Dido's problem l city of carthage l Mathspacetech

The isoperimetric problem is to determine a plane figure of the largest possible area whose boundary has a specified length.
The closely related Dido's problem asks for a region of the maximal area bounded by a straight line and a curvilinear arc whose endpoints belong to that line. It is named after Dido, the legendary founder and first queen of Carthage. The solution to the isoperimetric problem is given by a circle and was known already in Ancient Greece. However, the first mathematically rigorous proof of this fact was obtained only in the 19th century. Since then, many other proofs have been found.
The isoperimetric problem has been extended in multiple ways, for example, to curves on surfaces and to regions in higher-dimensional spaces. Perhaps the most familiar physical manifestation of the 3-dimensional isoperimetric inequality is the shape of a drop of water. Namely, a drop will typically assume a symmetric round shape. Since the amount of water in a drop is fixed, surface tension forces the drop into a shape which minimizes the surface area of the drop, namely a round sphere.
#maths
#isoperimetric
#applications of mathematics