See the ONE Math Concept That Powers ALL of AI (It's Easier Than You Think) - Lecture 4

🔄AIML Lecture Series :    • AIML  

🔄AI Math and Programming Series :    • AI Math and Programming  

🔔 Subscribe to the channel and turn on notifications so you never miss a new lesson!

Ever wondered how AI actually learns? The secret is calculus! In this video, we break down the essential calculus concepts that power modern artificial intelligence and machine learning.
What you'll learn:

How derivatives help AI optimize and learn from data
The role of gradients in training neural networks
Why backpropagation is just the chain rule in action
Real examples of calculus working behind the scenes in AI

Partial derivatives and gradient descent
The chain rule and backpropagation
Loss functions and optimization
How neural networks minimize error using calculus
Practical applications in deep learning

Perfect for computer science students, AI practitioners, or anyone wanting to understand the mathematical principles behind machine learning algorithms.

0:00 – 0:40 — AI Is Powered by Math

Everyday AI systems (GPS, recommendations, image generation) rely on deep learning, which is fundamentally powered by calculus + linear algebra.

0:41 – 1:30 — Core Idea: Minimizing Error

Training a neural network = finding parameter values (weights + biases) that minimize a loss function.

Loss function quantifies the network’s “wrongness.”

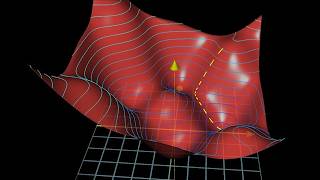
1:30 – 2:30 — The Optimization Problem

The error surface is high-dimensional and complex.

You need a systematic way to move toward lower error → enter gradients.

2:30 – 4:38 — Gradient Descent

Gradient = vector of partial derivatives → tells how to change parameters to reduce error.

Gradient Descent algorithm:

Compute gradient.

Move parameters against the gradient.

Repeat.

4:38 – 7:22 — Partial Derivatives in Many Dimensions

Each weight affects the output differently.

Partial derivatives measure the effect of each individual parameter on the loss.

Gradients combine all these partials into a single vector pointing “downhill.”

7:22 – 9:00 — Jacobian Matrices

When dealing with multi-input + multi-output functions, use the Jacobian.

It’s a matrix of derivatives that captures all dependencies at once.

Neural networks internally compute massive Jacobians.

9:00 – 12:36 — Chain Rule for Deep Networks

Each layer transforms the previous layer’s output.

To compute the gradient of the whole network:

Use the vector chain rule, which becomes:

Matrix multiplications of Jacobians.

This is exactly what backpropagation is.

12:36 – 15:24 — What a Neuron Actually Does

A neuron = weighted sum (linear) → nonlinear activation function.

This tiny unit, repeated many times, forms deep networks.

15:24 – 17:31 — Why Nonlinearity Matters

Stack of linear layers = still linear → useless.

Activations (ReLU, sigmoid, tanh) enable complex pattern modeling.

ReLU helps avoid vanishing gradients.

17:31 – 20:06 — ReLU and Vanishing Gradient

Sigmoid saturates → derivative ≈ 0 → gradients vanish.

ReLU’s derivative is large where active → strong learning signal.

20:06 – 24:40 — Universal Approximation

Deep networks with nonlinear activations can approximate any continuous function.

Foundation of AI’s representational power.

24:40 – 27:05 — Final Takeaways

Gradients are essential to training.

Matrix calculus + chain rule are the math engines behind deep learning.

Nonlinearity makes neural networks powerful.


👨‍💻 Who is this channel for?

Aspiring Data Scientists & ML Engineers: Solidify the core mathematical intuition that interviews and real-world projects demand.

Students: Struggling to see the connection between your linear algebra class and your AI ambitions? We make it crystal clear.

Curious Developers: You can import a library, but do you know what’s happening inside? Level up from a coder to a true creator.

Anyone Fascinated by AI: If you want to move beyond being a user of technology and become someone who understands it, this is your starting point.


#MachineLearning #Mathematics #ArtificialIntelligence #LinearAlgebra #Calculus #DeepLearning #DataScience #Tutorial #KNN #Regression #Classification #Python #AI #LearnToCode #techeducation

#AI #Calculus #MachineLearning #ArtificialIntelligence #Math #TechEducation #DeepLearning #DataScience #Programming