Demystifying Tensors
Автор: Gerard Meilan
Загружено: 2026-01-17
Просмотров: 14
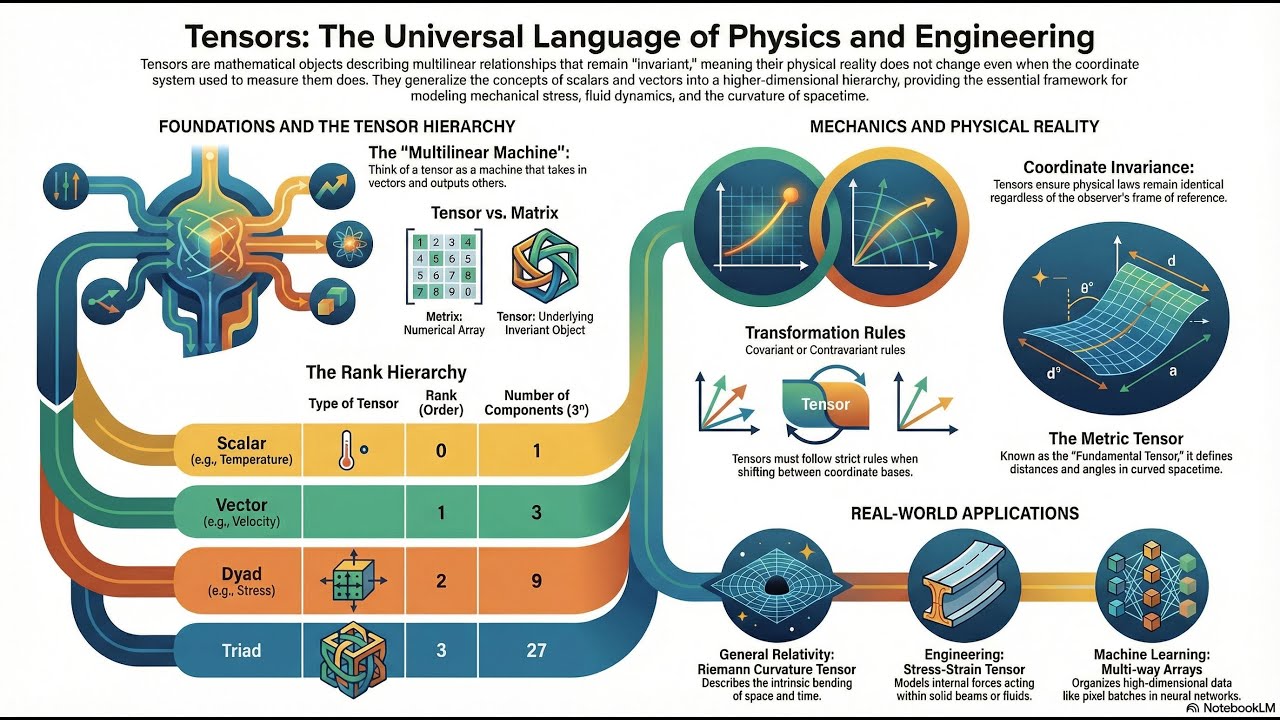
Tensors are fundamental algebraic objects that generalize scalars (rank 0) and vectors (rank 1) to higher orders, serving as coordinate-independent entities that describe physical or geometric properties objectively regardless of the observer's frame of reference. While they are often represented concretely as multidimensional arrays of components, a tensor is rigorously defined by the specific transformation laws (covariance and contravariance) these components obey when the underlying basis changes, ensuring the entity itself remains invariant. From a functional perspective, tensors act as multilinear maps that accept vectors and covectors as inputs to produce linear outputs, effectively modeling complex relationships—such as conductivity in crystals or curvature in spacetime—where input and output vectors may not be aligned. Ultimately, whether viewed as elements of a tensor product of vector spaces or as geometric objects defined by their transformation properties, tensors provide the necessary mathematical framework for formulating physical laws that hold true across different coordinate systems.
Доступные форматы для скачивания:
Скачать видео mp4
-
Информация по загрузке:



















