Reinforcement Learning, Model Predictive Control, and the Newton Step for Solving Bellman's Equation

Slides at https://web.mit.edu/dimitrib/www/MPC....

We focus on a conceptual framework that connects approximate Dynamic Programming (DP), Model Predictive Control (MPC), and Reinforcement Learning (RL). This framework centers around two algorithms, which are designed largely independently of each other and operate in synergy through the powerful mechanism of Newton's method. We call them the off-line training and the on-line play algorithms. The names are borrowed from some of the major successes
of RL involving games; primary examples are the recent (2017) AlphaZero program (which plays chess), and the similarly structured and earlier (1990s) TD-Gammon program (which plays backgammon). In these game contexts, the off-line training algorithm is the method used to teach the program how to evaluate positions and to generate good moves at any given position, while the on-line play algorithm is the method used to play in real time against human or computer opponents.

Significantly, the synergy between off-line training and on-line play also underlies MPC (as well as other major classes of sequential decision problems), and indeed the MPC design architecture is very similar to the one of AlphaZero and TD-Gammon. This conceptual insight provides a vehicle for bridging the cultural gap between RL and MPC, and sheds new light on some fundamental issues in MPC. These include the enhancement of stability properties through rollout, the treatment of uncertainty through the use of certainty equivalence, the resilience of MPC in adaptive control settings that involve changing system parameters, and the insights provided by the superlinear performance bounds implied by Newton's method.

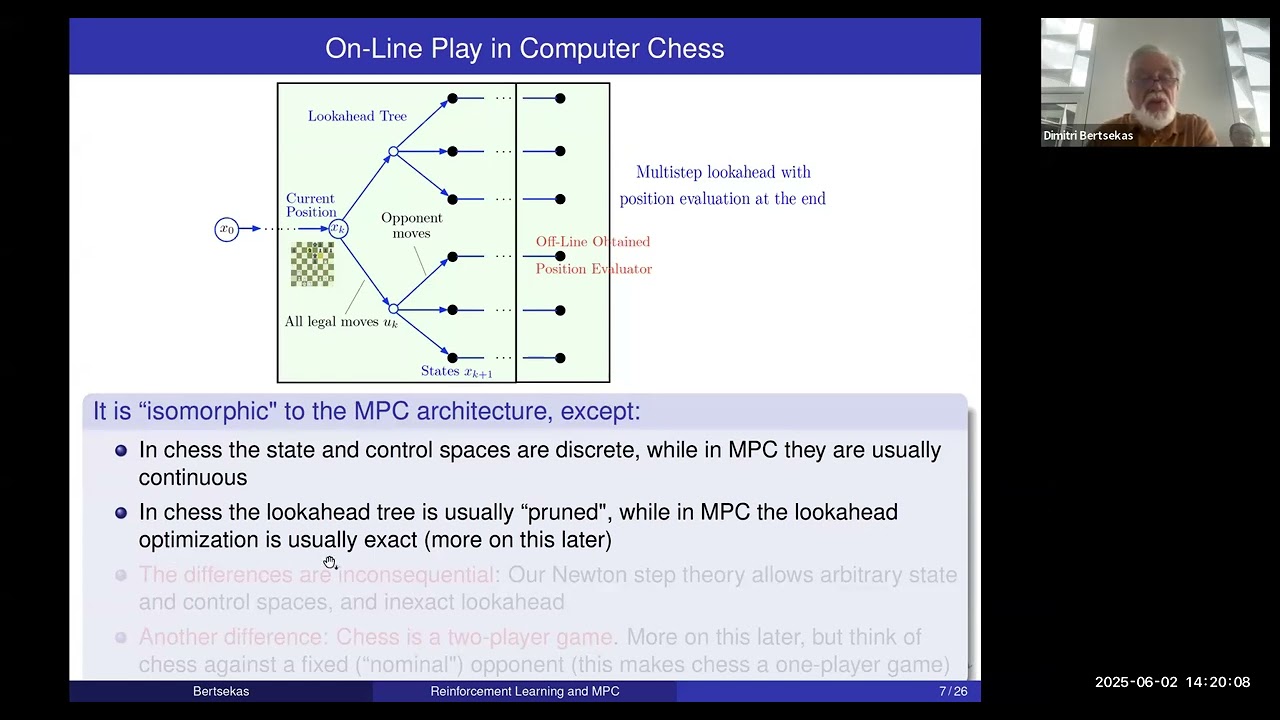
We discuss application contexts for our framework, including a computer chess architecture based on MPC.