Strain Energy Approach to Developing Stiffness Matrices in FEA (Castigliano's theorem)

The purpose of this video is to introduce a strain energy approach for developing stiffness matrices in Finite Element Analysis (FEA). While stiffness matrices for 1D elements such as trusses and beams can be developed using mechanics of materials methods, 2D and 3D elements require either energy or weighted residual approaches.

The particular approach shown in this video is Castigliano's theorem. The principle of minimum potential energy is used in a similar way but is not described specifically in this video.

0:00 General introduction
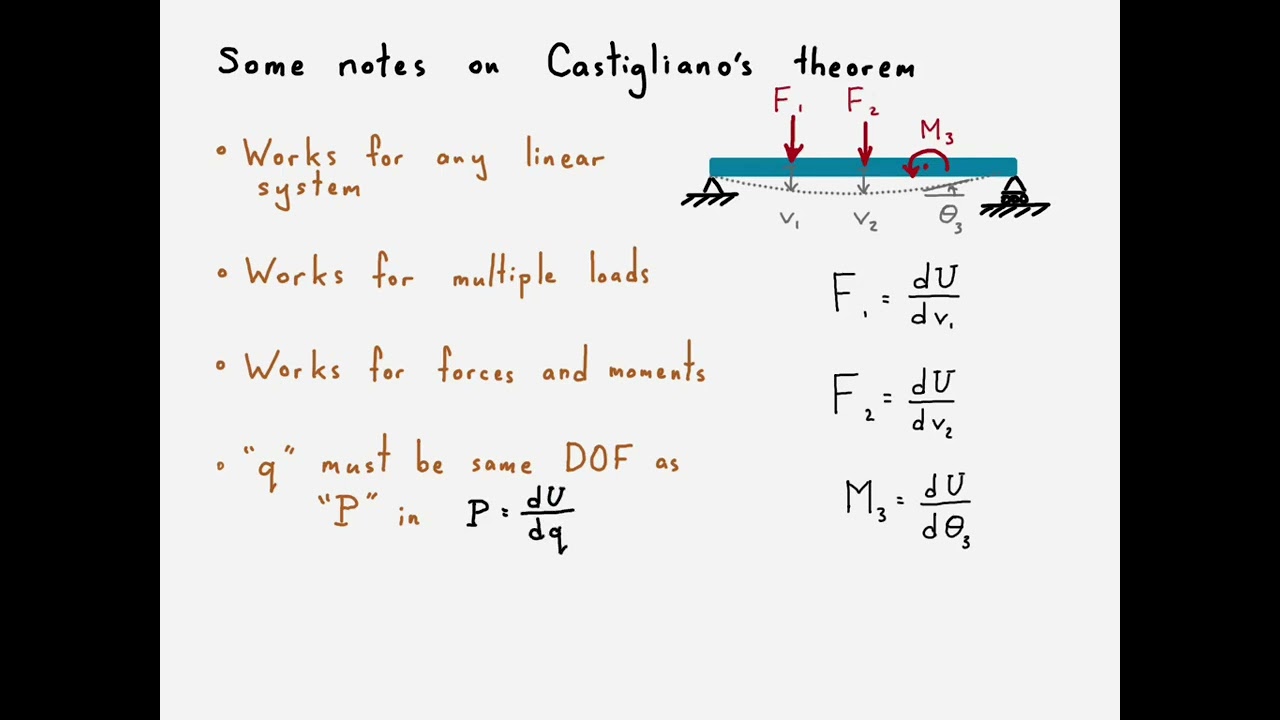
1:24 Description of Castigliano's theorem
4:23 Application of Castigliano's theorem to derive the truss element stiffness matrix
9:53 Reflection questions

Suggested answers to reflection questions:
1.) "P" can be either a discrete force or moment. "q" would then be either the displacement or rotation at the same location and same direction as "P" (i.e., it is the same degree of freedom as "P").
2.) "U" is the strain energy for the system. It needs to be in terms of individual nodal displacements (and possibly rotations) in order to apply Castigliano's theorem.
3.) Everything in the system is linearly elastic
4.) A frame element in 2D space has six degrees of freedom (3 DOF at each node - axial, transverse, and rotation). Therefore, Castigliano's would need to be applied six times to determine the stiffness matrix [K].